

L'objectif est d'exploiter certaines fonctionnalités du tableur permettant d'argumenter une prise de décision
| Vous pouvez soit visionner une petite vidéo, soit lire le texte plus détaillé ci-dessous |
 |
Mise en oeuvre :
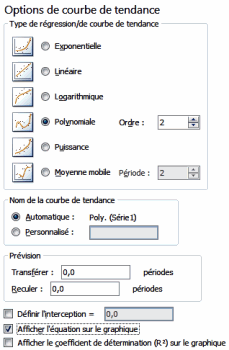
* "Ordre" ou "Degré"
selon le tableur.
Paramètres de la courbe de tendance sous MS Excel → |
 |
Remarques :
|
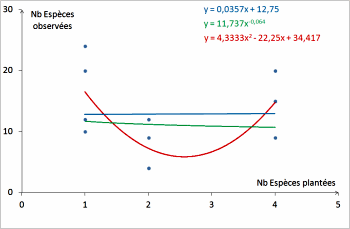
Coefficient de détermination R²Il est possible de tracer de nombreuses courbes de tendance sur un même nuage de points. Comment choisir la "moins mauvaise" ? |
 |
| MS Excel → |
| Le coefficient de détermination R², associé à chaque courbe de tendance, est une grandeur sans unité comprise entre 0 et 1. Il peut être affiché de la même manière que l'équation de la courbe. Le coefficient de détermination R² estime la proportion de la variation de Y expliquée par la variable X (autrement dit expliquée par le modèle) :
|
Equation et coeff. de détermination de nos 3 courbes de tendance |
||||||||||||
Avantage du coefficient de détermination R² : Très simple à utiliser Inconvénients (parmi beaucoup d'autres) :
|
|
Afficher le R², c'est bien, mais cela ne dispense pas de réfléchir ...Avec notre nuage de points, le coefficient de détermination est de 0,45. ce qui correspond à une régression "moyenne", ce qui est pas mal pour des données biologiques. Sauf que, pour s'approprier la technique, nous avons volontairement choisi un échantillon d'effectif très faible. Si on refait la régression polynomiale sur le
graphe des moyennes (image ci-contre), l'équation est la même
mais le R² est de ... 1,00. Le degré de l'équation est lié au nombre de paramètres insérés dans l'équation :
|
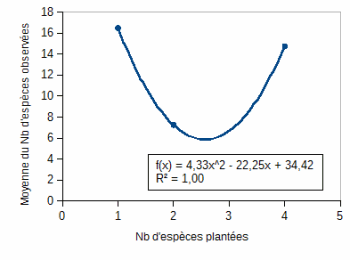 Sous Libre Office |
Plus le nombre de paramètres dans l'équation sera important, plus l'interprétation biologique du modèle construit sera complexe.
Conclusion : Refaire la manip avec plus d'années, plus
de types de parcelles et plus de parcelles de chaque type : les résultats
seront sensiblement différents !
En ayant en tête que si j'ai un grand nombre de points par (exemple n = 1000),
je peux toujours obtenir une régression mathématiquement "parfaite"
de degré n-1 = 999, mais sans interprétation
biologique possible...
